Advertisements
Advertisements
प्रश्न
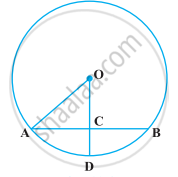
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to ______.
विकल्प
2 cm
3 cm
4 cm
5 cm
उत्तर
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to 2 cm.
Explanation:

We know that, the perpendicular from the centre of a circle to a chord bisects the chord.
AC = CB = `1/2` AB = `1/2` × 8 = 4 cm
Given OA = 5 cm
AO2 = AC2 + OC2
(5)2 = (4)2 + OC2
25 = 16 + OC2
OC2 = 25 – 16 = 9
OC = 3 cm ...[Taking positive square root, because length is always positive]
OA = OD ...[Same radius of a circle]
OD = 5 cm
CD = OD – OC
= 5 – 3
= 2 cm
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
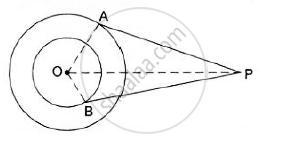
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
The ______________ is the longest chord of a circle
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

In the given figure, O is the centre of the circle. Name all radii of the circle.