Advertisements
Advertisements
प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

उत्तर

Given: AB and CD are common tangents to both the circles.
To prove: AB = CD
Proof:
We know that two tangents drawn to a circle for the same exterior point are
equal.
Thus we get
AE = EC (i)
Similarly
ED = EB (ii)
AB = AE + EB (iii)
and
CD = CE + ED (iv)
AB = EC + EB from (i) and (iii)
CD = EC + EB from (ii) and (iv)
Therefore AB = CD
Hence proved.
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
A circle is a plane figure.
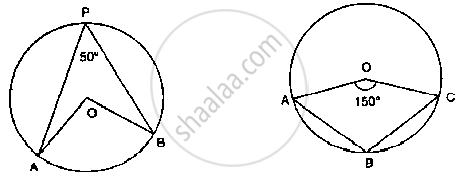
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
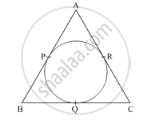
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
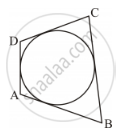
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Use the figure given below to fill in the blank:
______ is a chord of the circle.

A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
From the figure, identify a diameter.
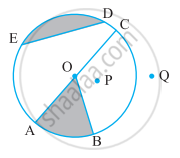
From the figure, identify a point in the exterior.

