Advertisements
Advertisements
प्रश्न
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
उत्तर
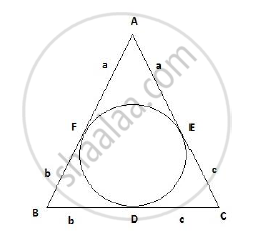
Given: ABC is an isosceles triangle in which AB = AC; with a circle inscribed
in the triangle.
To prove: BD = DC
Proof:
AF and AE are tangents drawn to the circle from point A.
Since two tangents drawn to a circle from the same exterior point are equal,
AF = AE = a
Similarly BF = BD = b and CD = CE = c
We also know that Δ ABC is an isosceles triangle in which AB = AC.
a+b = a+c
Thus b = c
Therefore, BD = DC
Hence proved.
APPEARS IN
संबंधित प्रश्न
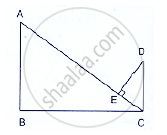
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
In an equilateral triangle ABC if AD ⊥ BC, then
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
