Advertisements
Advertisements
प्रश्न
In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
उत्तर
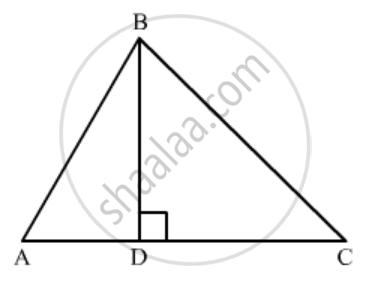
Since Δ ADB is right triangle right angled at D
`AB^2=AD^2+BD^2`
In right Δ BDC, we have
`CD^2+BD^2=BC^2`
Sine `2AC.DC=BC^2`
`⇒DC^2+BD^2=2AC.DC `
`2AC.DC=AC^2-AC^2+DC^2+BD^2`
`AC^2=AC^2+DC^2-2AC.DC+BD^2`
`AC^2=(AC-DC)^2+BD^2`
`AC^2=AD^2+BD^2`
Now substitute `AD^2+BD^2=AB^2`
`AC^2=AB^2`
`AC=AB`
APPEARS IN
संबंधित प्रश्न
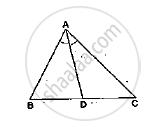
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

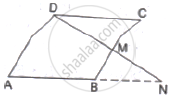
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
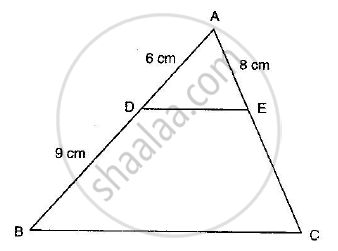
In the adjoining figure, find AC.
State SAS similarity criterion.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
