Advertisements
Advertisements
प्रश्न
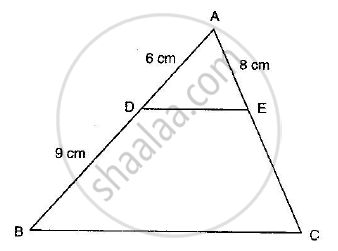
In the adjoining figure, find AC.
उत्तर
GIVEN: In the figure we are given AD = 6cm, BD = 9cm, AE = 8cm
TO FIND: AC
According to BASIC PROPORTIONALITY THEOREM, if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ABC, DE || BC. So,
`(AD)/(DB)=(AE)/(EC)`
`6/9=8/(EC)`
`EC=(8xx9)/6`
`EC=12cm`
Now,
`AC=AE+EC`
`AC=8+12`
`AC=20cm`
APPEARS IN
संबंधित प्रश्न
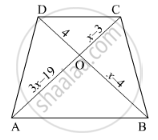
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
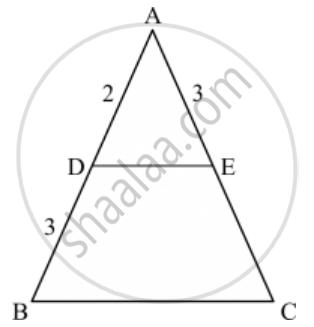
In the given figure, if ∠ADE = ∠ABC, then CE =
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
In the given figure, Δ AHK ∼ Δ ABC. If AK = 8 cm, BC = 3.2 cm and HK = 6.4 cm, then find the length of AC.

