Advertisements
Advertisements
प्रश्न
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
उत्तर
Since ` ∆DMU ∼ ∆BMV`
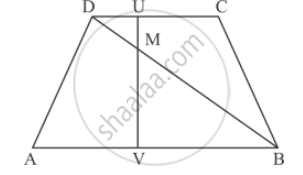
`(DM)/(BM)=(MU)/(MV)=(DU)/(BV)`
`(DM)/(BM)=(DU)/(BV)`
By cross multiplication, we get `DMxxBVxxDUxxBM`
Hence proved that `DMxxBVxxDUxxBM`
APPEARS IN
संबंधित प्रश्न
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
In an equilateral triangle ABC if AD ⊥ BC, then
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
