Advertisements
Advertisements
प्रश्न
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
उत्तर
In trapezium ABCD, AB || DC. P and Q are points on sides AD and BC such that PQ || AB.
Join AC. Suppose AC intersects PQ in O.
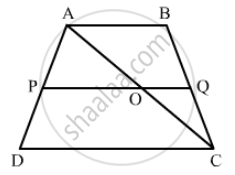
In Δ ACD , OP || CD
`∴ (AP)/(PD)=(AO)/(OC)`.......(1) (BPT)
`In Δ Abc , OQ||AB`
`∴ (BQ)/(QC)=(AO)/(OC)`.......(2) (BPT)
From (1) and (2), we get
`(AP)/(DP)=(BQ)/(QC)`
`(AP)/(18)=(35)/(15)`
`AP=(35xx18)/(5xx3)`
`AP=(7xx5xx3xx6)/(5xx3)`
`AP=(7xxcancel5xxcancel3xx6)/(cancel5xxcancel3)`
`AP = 42`
`AD=AP+PD`
`AD=42+18`
`AD=60`
Hence, the value of AD is 60 .
APPEARS IN
संबंधित प्रश्न
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
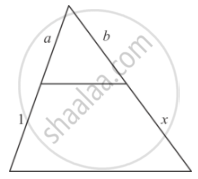
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
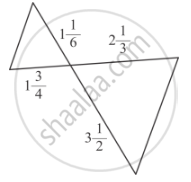
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
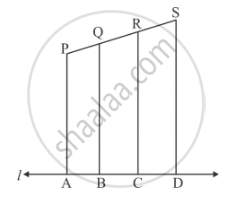
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
