Advertisements
Advertisements
प्रश्न
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
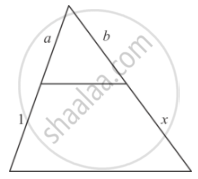
उत्तर
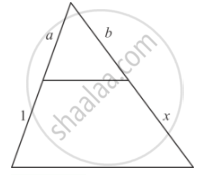
`a/(a+1)=b/(b+x)`
By cross multiplication on both sides, we get
`axx(b+x)=bxx(a+1)`
`ab+ax=ab+b`
`ax=ab+b-ab`
`ax=cancel(ab)+b-cancel(ab)`
`ax=b`
`x=b/a`
Hence the value of x is `b/a`
APPEARS IN
संबंधित प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
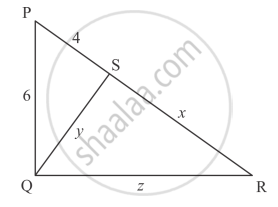
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
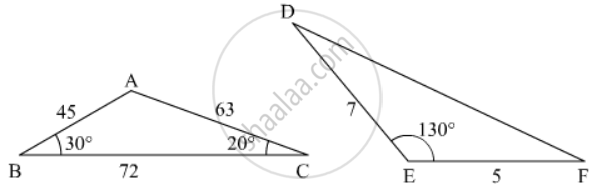
In the given figure the measure of ∠D and ∠F are respectively
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
