Advertisements
Advertisements
प्रश्न
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
उत्तर
We are given ABCD is a trapezium with AB||DC
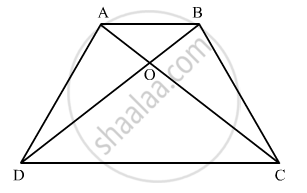
Consider the triangles AOB and COD in which
`∠ AOB = ∠COD `
`∠ ABO = ∠ODC ` (ALTERNATIVE ANGLE)
`∠ BAO = ∠DCA ` (ALTERNATIVE ANGLE)
Therefore, ` ∆ODC ∼ ∆ OBA`
`⇒ (AO)/(OC)=(BO)/(DO)=(AB)/(CD)`
`⇒ (AO)/(OC)=(BO)/(DO) `
Hence we have proved that O, the point of intersection of diagonals, divides the two diagonals in the same ratio.
We are given AB = 3CD and we have to prove that `(ar∆ OCD)/(ar∆ OAB)=1/9`
We already have proved that AOB and COD are similar triangles
So
`(ar∆ OCD)/(ar∆ OAB)= (CD^2)/(AB^2)`
`(ar∆ OCD)/(ar∆ OAB)= (CD^2)/(3CD^2)`
`(ar∆ OCD)/(ar∆ OAB)= 1/9`
Hence, Prove that `(ar∆ OCD)/(ar∆ OAB)= 1/9`
APPEARS IN
संबंधित प्रश्न
In below figure, If AB || CD, find the value of x.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
State SSS similarity criterion.
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
