Advertisements
Advertisements
प्रश्न
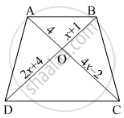
In below figure, If AB || CD, find the value of x.
उत्तर
Since diagonals of a trapezium divide each other proportionally.
`therefore"AO"/"OC"="BO"/"OD"`
`rArr4/(4x-2)=(x+1)/(2x+4)`
⇒ 4(2𝑥 + 4) = (𝑥 + 1)(4𝑥 − 2)
⇒ 8x + 16 = x(4x – 2) +1(4x – 2)
⇒ 8x + 16 = 4x2 + 2x – 2
⇒ 4x2 + 2𝑥 − 8𝑥 − 2 − 16 = 0
⇒ 4x2 − 6𝑥 − 18 = 0
⇒ 2[2𝑥2 − 3𝑥 − 9] = 0
⇒ 2𝑥2 − 3𝑥 − 9 = 0
⇒ 2𝑥(𝑥 − 3) + 3(𝑥 − 3) = 0
⇒ (𝑥 − 3)(2𝑥 + 3) = 0
⇒ 𝑥 − 3 = 0 or 2𝑥 + 3 = 0
⇒ 𝑥 = 3 or 𝑥 = -3/2
𝑥 = -3/2 is not possible, because
`"OB"=x+1=-3/2+1=-1/2`
Length cannot be negative
`therefore"AO"/"OC"="BO"/"OD"`
APPEARS IN
संबंधित प्रश्न
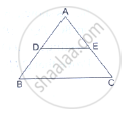
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
State Pythagoras theorem and its converse.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
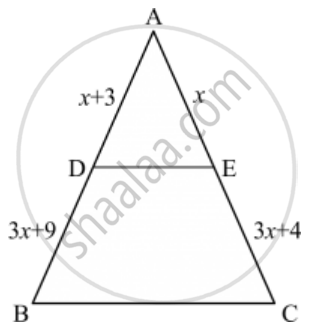
In the given figure, the value of x for which DE || AB is
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
