Advertisements
Advertisements
प्रश्न
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
विकल्प
AQ2 + CP2 = 2(AC2 + PQ2)
2(AQ2 + CP2) = AC2 + PQ2
AQ2 + CP2 = AC2 + PQ2
\[AQ + CP = \frac{1}{2}\left( AC + PQ \right)\]
उत्तर
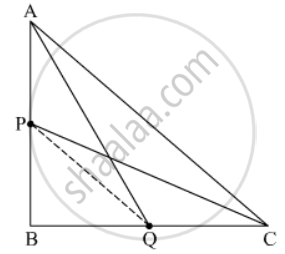
Applying Pythagoras theorem,
In ΔAQB,
In ΔPBC
`CP^2=PB^2+BC^2`..............(2)
Adding (1) and (2), we get
\[{AQ}^2 + {CP}^2 = {AB}^2 + {BQ}^2 + {PB}^2 + {BC}^2 \]....(3)
In ΔABC,
`AC^2=AB^2+BC^2`....(4)
In ΔPBQ,
From (3), (4) and (5), we get
We got the result as `c`
Notes
Disclaimer: There is mistake in the problem. The question should be "In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and BC respectively, then"
Given: In the right ΔABC, right angled at B. P and Q are points on the sides AB and BC respectively.
APPEARS IN
संबंधित प्रश्न
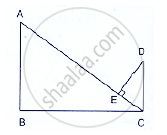
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
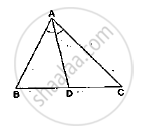
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
What values of x will make DE || AB in the given figure?

The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
