Advertisements
Advertisements
प्रश्न
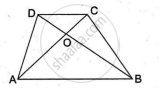
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Show that `"OA"/"OC"="OB"/"OD"`.
उत्तर

We have,
ABCD is a trapezium with AB || DC
In ΔAOB and ΔCOD
∠AOB = ∠COD ...[Vertically opposite angles]
∠OAB = ∠OCD ...[Alternate interior angles]
Then, ΔAOB ~ ΔCOD ...[By AA similarity]
`therefore"OA"/"OC"="OB"/"OD"` ...[Corresponding parts of similar Δ are proportional.]
APPEARS IN
संबंधित प्रश्न
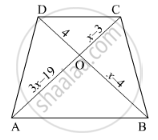
In below figure, If AB || CD, find the value of x.
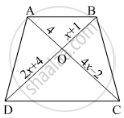
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
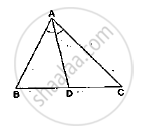
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
What values of x will make DE || AB in the given figure?

In the given figure, DE || BD. Determine AC and AE.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
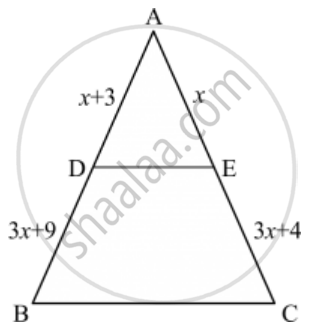
In the given figure, the value of x for which DE || AB is
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
