Advertisements
Advertisements
प्रश्न
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
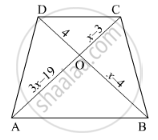
उत्तर
Since diagonals of a trapezium divide each other proportionally.
`therefore"AO"/"OC"="BO"/"OD"`
`rArr(3x-19)/(x-3)=(x-4)/4`
⇒ 4(3𝑥 − 19) = (𝑥 − 4)(𝑥 − 3)
⇒ 12x – 76 = x (x – 3) −4(x – 3)
⇒ 12𝑥 − 76 = 𝑥2 − 3𝑥 − 4𝑥 + 12
⇒ 𝑥2 − 7𝑥 − 12𝑥 + 12 + 76 = 0
⇒ 𝑥2 − 19𝑥 + 88 = 0
⇒ 𝑥2 − 11x − 8x + 88 = 0
⇒ 𝑥(𝑥 − 11) − 8(𝑥 − 11) = 0
⇒ (𝑥 − 11)(𝑥 − 8) = 0
⇒ 𝑥 − 11 = 0 or x – 8 = 0
⇒ x = 11 or x = 8
APPEARS IN
संबंधित प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

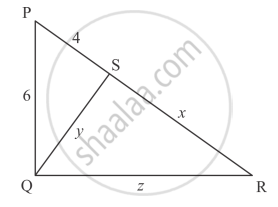
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
State basic proportionality theorem and its converse.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
State Pythagoras theorem and its converse.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

