Advertisements
Advertisements
प्रश्न
In the below figure, If AB || CD, find the value of x.
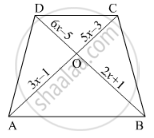
उत्तर
`rArr(3x-1)/(5x-3)=(2x+1)/(6x-5)`
⇒ (3x – 1) (6x – 5) = (2x + 1) (5x – 3)
⇒ 3x (6x – 5) – 1(6x – 5) = 2x (5x – 3) + 1 (5x – 3)
⇒ 18𝑥2 − 15𝑥 − 6𝑥 + 5 = 10𝑥2 − 6𝑥 + 5𝑥 − 3
⇒ 8𝑥2 − 20𝑥 + 8 = 0
⇒ 4(2𝑥2 − 5𝑥 + 2) = 0
⇒ 2𝑥2 − 4𝑥 − 1𝑥 + 2 = 0
⇒ 2𝑥(𝑥 − 2) − 1(𝑥 − 2) = 0
⇒ (2𝑥 − 1)(𝑥 − 2) = 0
⇒ 2x – 1 = 0 or x – 2 = 0
⇒ 𝑥 = 1/2 or 𝑥 = 2
𝑥 = 1/2 is not possible, because, OC = 5x – 3
`= 5(1/2) - 3`
`=(5-6)/2=-1/2`
APPEARS IN
संबंधित प्रश्न
In the given figure,
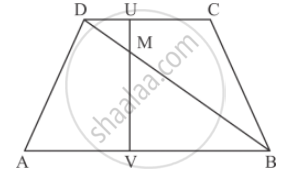
AB || DC prove that
DM × BV = BM ✕ DU
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
State basic proportionality theorem and its converse.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.
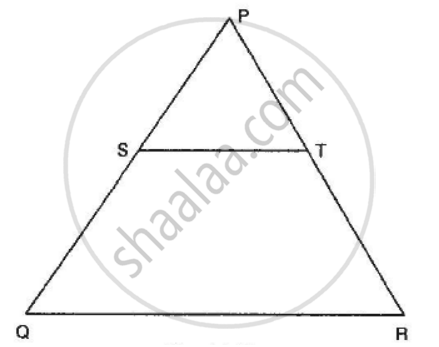
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.
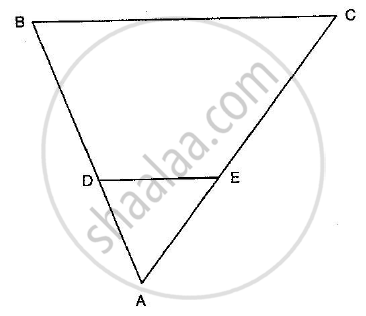
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
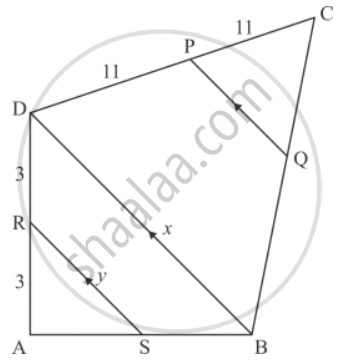
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
