Advertisements
Advertisements
प्रश्न
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
उत्तर
In ΔABC , BN ⊥ AC.
Also, `BN^2=ANxxNC`
We have to prove that `∠ B= 90^o`.

In triangles ABN and BNC, we have
`AB^2=AN^2+BN^2`
`BC^2=BN^2+CN^2`
Adding above two equations, we get
`AB^2+BC^2=AN^2+CN^2+2BN^2`
Since `BN^2= AN.NC`
So,
`AB^2+BC^2=AN^2+CN^2+2BN^2`
`AB^2+BC^2=(AN+NC)^2`
`AB^2+BC^2=AC^2`
Hence `∠ B = 90^o`
APPEARS IN
संबंधित प्रश्न
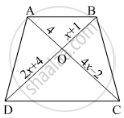
In below figure, If AB || CD, find the value of x.
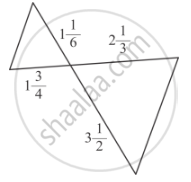
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
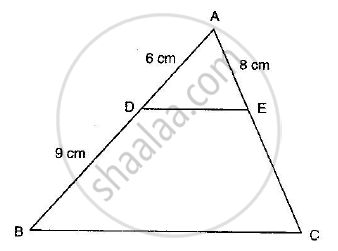
In the adjoining figure, find AC.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
In an equilateral triangle ABC if AD ⊥ BC, then
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
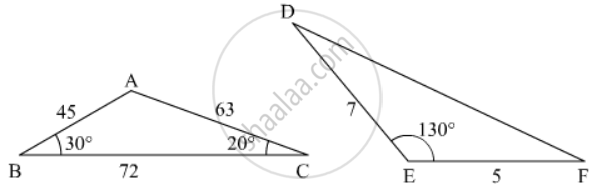
In the given figure the measure of ∠D and ∠F are respectively
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
