Advertisements
Advertisements
Question
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
Solution
In ΔABC , BN ⊥ AC.
Also, `BN^2=ANxxNC`
We have to prove that `∠ B= 90^o`.

In triangles ABN and BNC, we have
`AB^2=AN^2+BN^2`
`BC^2=BN^2+CN^2`
Adding above two equations, we get
`AB^2+BC^2=AN^2+CN^2+2BN^2`
Since `BN^2= AN.NC`
So,
`AB^2+BC^2=AN^2+CN^2+2BN^2`
`AB^2+BC^2=(AN+NC)^2`
`AB^2+BC^2=AC^2`
Hence `∠ B = 90^o`
APPEARS IN
RELATED QUESTIONS
In below figure, If AB || CD, find the value of x.
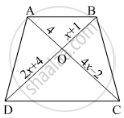
In the below figure, If AB || CD, find the value of x.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
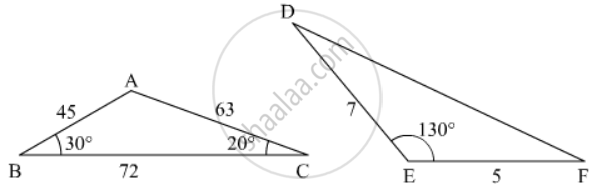
In the given figure the measure of ∠D and ∠F are respectively