Advertisements
Advertisements
Question
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
Solution
Since BC = CD + BD
`⇒ CD =BC -BD`
`CD = a - (ac)/(b+c)`
`= (ab)/(b+c)`
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
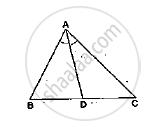
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
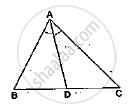
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
