Advertisements
Advertisements
Question
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

Solution
We are given the following figure with the related information
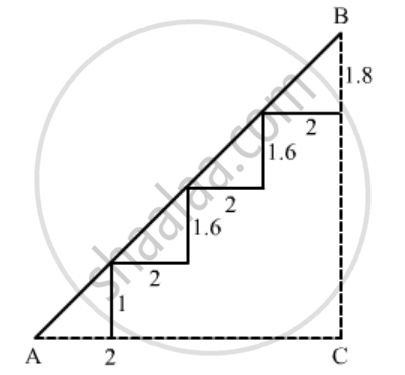
In the above figure complete the triangle ABC with right angled at C
So
AC = 2 + 2 + 2 + 2 = 8 and
BC = 1 + 1.6 + 1.6 + 1.8 = 6
Using Pythagoras theorem for triangle ABC to find
`AB^2=AC^2+BC^2`
`=8^2+6^2`
`=100`
`⇒ AB=10`
Hence the distance between A and B is 10 cm.
APPEARS IN
RELATED QUESTIONS
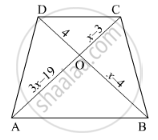
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
