Advertisements
Advertisements
Question
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
Options
3 : 4
4 : 3
2 : 3
4 : 5
Solution
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is 3 : 4.
Explanation:
Given: Areas of two similar triangles are 9cm2 and 16cm2.
To find: Ratio of their corresponding sides.
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`\text{ar(tringle 1)}/\text{ar(tringle 2)}=(\text{side1}/\text{side2})^2`
`9/16 = (\text{side1}/\text{side2})^2`
Taking square root on both sides, we get
So, the ratio of their corresponding sides is 3 : 4.
Hence the correct answer is `a`
APPEARS IN
RELATED QUESTIONS
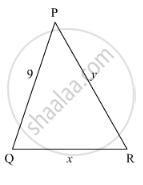
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
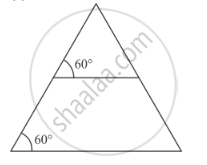
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the road. Assuming that her string (from the tip of her road to the fly) is taut, how much string does she have out (in the given figure)? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

State SAS similarity criterion.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
