Advertisements
Advertisements
Question
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
Solution
GIVEN: ΔABC and ΔDEF are similar triangles such that AB = 3cm, BC = 2cm, CA = 2.5cm and EF = 4cm.
TO FIND: Perimeter of ΔDEF.
We know that if two triangles are similar then their corresponding sides are proportional.
Hence, `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`
Substituting the values, we get
`(AB)/(BC)=(DE)/(EF)`
`3/2=(DE)/4`
`DE=6 cm`........(1)
Similarly,
`(CA)/(BC)=(DF)/(EF)`
`2.5/2=(DF)/(4)`
`DF= 5cm`...........(2)
P[erimeter of `Δ DEF = DE +EF+DF`
`=6+4+5`
`= 15 cm`
APPEARS IN
RELATED QUESTIONS
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
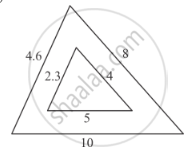
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
