Advertisements
Advertisements
Question
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
Solution
GIVEN: ΔABC and ΔDEF are two triangles such that .
TO FIND: Area (ABC) : Area (DEF)
We know that two triangles are similar if their corresponding sides are proportional.
Here, ΔABC and ΔDEF are similar triangles because their corresponding sides are given proportional, i.e. \[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\]
Since the ratio of the areas of two similar triangle is equal to the ratio of the squares of their corresponding sides.
`⇒ (Area(Δ ABC))/(Area(Δ DEF))=9/12`
APPEARS IN
RELATED QUESTIONS
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
What values of x will make DE || AB in the given figure?

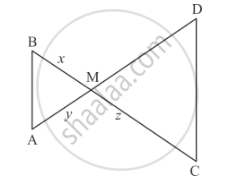
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
