Advertisements
Advertisements
प्रश्न
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
उत्तर
GIVEN: ΔABC and ΔDEF are two triangles such that .
TO FIND: Area (ABC) : Area (DEF)
We know that two triangles are similar if their corresponding sides are proportional.
Here, ΔABC and ΔDEF are similar triangles because their corresponding sides are given proportional, i.e. \[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\]
Since the ratio of the areas of two similar triangle is equal to the ratio of the squares of their corresponding sides.
`⇒ (Area(Δ ABC))/(Area(Δ DEF))=9/12`
APPEARS IN
संबंधित प्रश्न
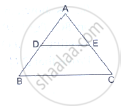
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
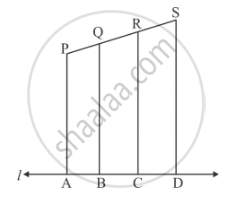
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
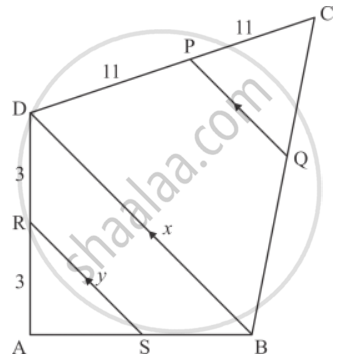
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.