Advertisements
Advertisements
प्रश्न
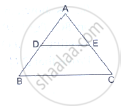
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
उत्तर
We have:
AB = 10.8 cm, AD = 6.3 cm
Therefore,
DB = 10.8 – 6.3 = 4.5 cm
Similarly,
AC = 9.6 cm, EC = 4cm
Therefore,
AE = 9.6 – 4 = 5.6 cm
Now,
`(AD)/(DB)=6.3/4.5=7/5`
`(AE)/(EC)=5.6/4=7/5`
⟹`(AD)/(DB)=(AE)/(EC)`
Applying the converse of Thales’ theorem,
We conclude that DE ‖ BC.
APPEARS IN
संबंधित प्रश्न
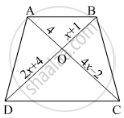
In below figure, If AB || CD, find the value of x.
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
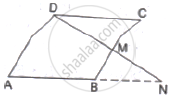
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
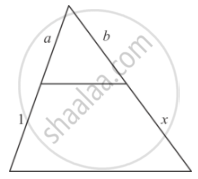
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
State basic proportionality theorem and its converse.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
