Advertisements
Advertisements
प्रश्न
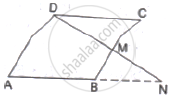
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
उत्तर
(i) Given: ABCD is a parallelogram
To prove :
(1)`(DM)/(MN)=(DC)/(BN)`
(2) `(DN)/(DM)=(AN)/(DC)`
Proof: In Δ DMC and Δ NMB
∠DMC = ∠NMB (Vertically opposite angle)
∠DCM = ∠NBM (Alternate angles)
By AAA- Similarity
ΔDMC ~ ΔNMB
∴`( DM)/(MN)=(DC)/(BM)`
NOW, `(MN)/(DM)+(BN)/(DC)`
Adding 1 to both sides, we get
`(MN)/(DM)+1=(BN)/(DC)+1`
⟹ `(MN+DM)/(DM)=(BN+DC)/(DC)`
⟹ `(MN+DM)/(DM)=(BN+AB)/(DC)` [∵ ABCD is a parallelogram]
⟹ `(DN)/(DM)=(AN)/(DC)`
APPEARS IN
संबंधित प्रश्न
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
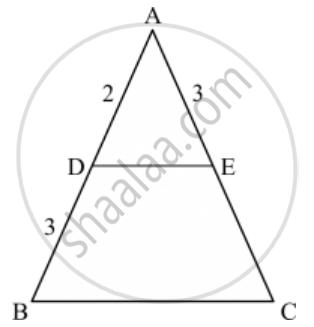
In the given figure, if ∠ADE = ∠ABC, then CE =
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
