Advertisements
Advertisements
प्रश्न
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
उत्तर
Let the trapezium be ABCD with E and F as the mid Points of AD and BC, Respectively Produce AD and BC to Meet at P.
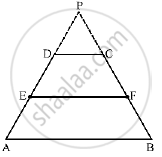
In Δ PAB, DC || AB.
Applying Thales’ theorem, we get
`(PD)/(DA)=(PC)/(CB)`
Now, E and F are the midpoints of AD and BC, respectively
⇒ `(PD)/(2DE)=(PC)/(2CF)`
⟹ `(PD)/(DE)=(PC)/(CF)`
Applying the converse of Thales’ theorem in Δ PEF, we get that DC
Hence, EF || AB.
Thus. EF is parallel to both AB and DC.
This completes the proof.
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
In fig, seg DE || sec BC, identify the correct statement.

ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.