Advertisements
Advertisements
प्रश्न
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
उत्तर
Let the trapezium be ABCD with E and F as the mid Points of AD and BC, Respectively Produce AD and BC to Meet at P.
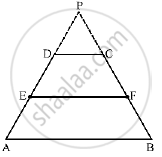
In Δ PAB, DC || AB.
Applying Thales’ theorem, we get
`(PD)/(DA)=(PC)/(CB)`
Now, E and F are the midpoints of AD and BC, respectively
⇒ `(PD)/(2DE)=(PC)/(2CF)`
⟹ `(PD)/(DE)=(PC)/(CF)`
Applying the converse of Thales’ theorem in Δ PEF, we get that DC
Hence, EF || AB.
Thus. EF is parallel to both AB and DC.
This completes the proof.
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In below Fig., state if PQ || EF.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x – 1) cm.
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
In ΔABC, AB = 6 cm and DE || BC such that AE = `1/4` AC then the length of AD is ______.
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.