Advertisements
Advertisements
प्रश्न
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
उत्तर
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.
Here, ΔBMP ~ ΔCNR
∴` (BM)/(CN)=(BP)/(CR)=(MP)/(NR)` ...........(1)
NOW`(BM)/(CN)=(MP)/(NR)` [𝑈𝑠𝑖𝑛𝑔 (1)]
⇒ `CN=(BMxxNR)/(MP)=(9xx9)/6=13.5 cm`
𝐴𝑔𝑎𝑖𝑛, `(BM)/(CN)=(BP)/(CR)` [𝑈𝑠𝑖𝑛𝑔 (1)]
⇒ `CR=(BPxxCN)/(BM)=(5xx13.5)/9=7.5 cm`
Perimeter of ΔCNR = CN + NR + CR = 13.5 + 9 + 7.5 = 30 cm
APPEARS IN
संबंधित प्रश्न
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
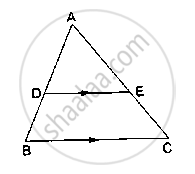
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
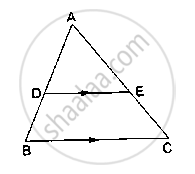
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

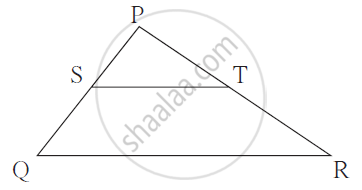
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`
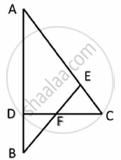
State and prove Basic Proportionality theorem.
