Advertisements
Advertisements
प्रश्न
In the given figure MN|| BC and AM: MB= 1: 2
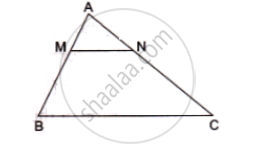
find ` (area(ΔAMN))/(area(ΔABC))`
उत्तर
We have
AM : MB = 1 : 2
⇒ AM:MB=1:2
⇒ `(MB)/(AM)=2/1`
Adding 1 to both sides, we get
⇒`( MB)/(AM)+1=2/1+1`
⇒`(MB+AM)/(AM)=(2+1)/1`
⇒ `(AB)/(AM)=3/1`
Now, In ΔAMN and ΔABC
∠𝐴𝑀𝑁 = ∠𝐴𝐵𝐶 (𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑎𝑛𝑔𝑙𝑒𝑠 𝑖𝑛 𝑀𝑁 ∥ 𝐵𝐶)
∠𝐴𝑁𝑀 = ∠𝐴𝐶𝐵 (𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑎𝑛𝑔𝑙𝑒𝑠 𝑖𝑛 𝑀𝑁 ∥ 𝐵𝐶)
By AA similarity criterion, ΔAMN ~ Δ ABC
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴`( area (Δ AMN))/(area(ΔABC))=((AM)/(AB))^2=(1/3)^2=1/9`
APPEARS IN
संबंधित प्रश्न
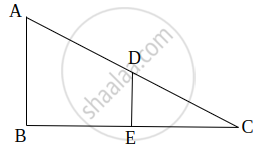
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
State the two properties which are necessary for given two triangles to be similar.
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
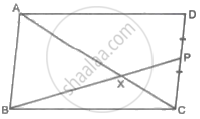
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.