Advertisements
Advertisements
Question
In the given figure MN|| BC and AM: MB= 1: 2
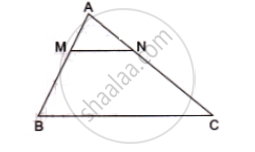
find ` (area(ΔAMN))/(area(ΔABC))`
Solution
We have
AM : MB = 1 : 2
⇒ AM:MB=1:2
⇒ `(MB)/(AM)=2/1`
Adding 1 to both sides, we get
⇒`( MB)/(AM)+1=2/1+1`
⇒`(MB+AM)/(AM)=(2+1)/1`
⇒ `(AB)/(AM)=3/1`
Now, In ΔAMN and ΔABC
∠๐ด๐๐ = ∠๐ด๐ต๐ถ (๐ถ๐๐๐๐๐ ๐๐๐๐๐๐๐ ๐๐๐๐๐๐ ๐๐ ๐๐ โฅ ๐ต๐ถ)
∠๐ด๐๐ = ∠๐ด๐ถ๐ต (๐ถ๐๐๐๐๐ ๐๐๐๐๐๐๐ ๐๐๐๐๐๐ ๐๐ ๐๐ โฅ ๐ต๐ถ)
By AA similarity criterion, ΔAMN ~ Δ ABC
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴`( area (Δ AMN))/(area(ΔABC))=((AM)/(AB))^2=(1/3)^2=1/9`
APPEARS IN
RELATED QUESTIONS
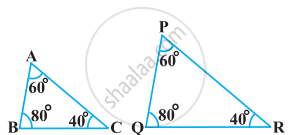
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
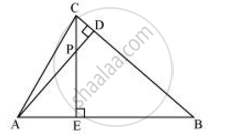
ΔAEP ∼ ΔCDP
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
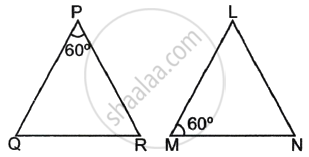
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅ `square`
⇒ ∠L = `square`
We know, the sum of angles of a triangle = `square`
∴ ∠L + ∠M + ∠N = `square`
Substituting the values of ∠L and ∠M in equation (i),
`square` + `square` + ∠N = `square`
∠N + `square` = `square`
∠N = `square` – `square`
∠N = `square`
Hence, the measure of ∠N is `square`.
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.
If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
