Advertisements
Advertisements
Question
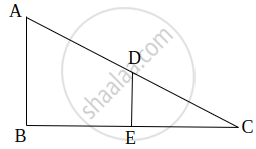
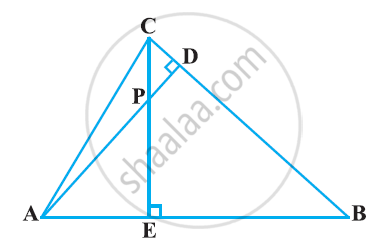
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
ΔAEP ∼ ΔCDP
Solution
In ΔAEP and ΔCDP,
∠AEP = ∠CDP ...(Each 90°)
∠APE = ∠CPD ...(Vertically opposite angles)
Hence, by using AA similarity criterion,
ΔAEP ∼ ΔCDP
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
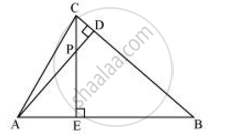
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
ΔAEP ∼ ΔADB
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
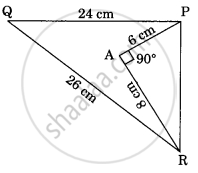
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.