Advertisements
Advertisements
Question
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
Solution
P = (a-1) cm, q = `2sqrta` 𝑐𝑚 𝑎𝑛𝑑 𝑟=(𝑎+1)𝑐𝑚
Then,
`p^2+q^2=(0a-1)^2+(2sqrta)^2`
=`a^2+1-2a+4a`
=`a^2+1+2a`
=`(a+1)^2`
`r^2=(a+1)^2`
`p^2+q^2=r^2`
Thus, the given triangle is right-angled.
APPEARS IN
RELATED QUESTIONS
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
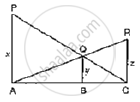
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?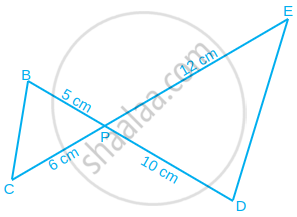
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).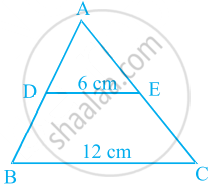
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

