Advertisements
Advertisements
Question
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).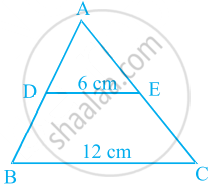
Solution
Given,
DE || BC,
DE = 6 cm
And BC = 12 cm
In ΔABC and ΔADE,
∠ABC = ∠ADE ...[Corresponding angle]
∠ACB = ∠AED ...[Corresponding angle]
And ∠A = ∠A ...[Common side]
∴ ΔABC ∼ ΔAED ...[By AAA similarity criterion]
Then, `("ar(ΔADE)")/("ar(ΔABC)") = ("DE")^2/("BC")^2`
= `(6)^2/(12)^2`
= `(1/2)^2`
⇒ `("ar(ΔADE)")/("ar(ΔABC)") = (1/2)^2 = 1/4`
Let ar(ΔADE) = k,
Then ar(ΔABC) = 4k
Now, ar(DECB) = ar(ABC) – ar(ΔADE)
= 4k – k
= 3k
∴ Required ratio = ar(ADE) : ar(DECB)
= k : 3k
= 1 : 3
APPEARS IN
RELATED QUESTIONS
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
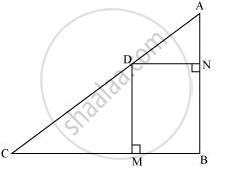
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
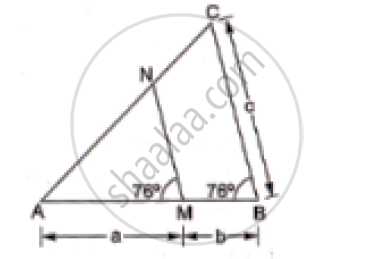
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?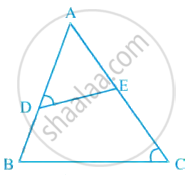
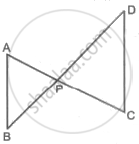
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
Which of the following conditions is not sufficient to determine the congruence of two triangles?
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

