Advertisements
Advertisements
Question
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.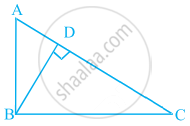
Solution
Given, ΔABC in which ∠B = 90° and BD ⊥ AC
Also, AD = 4 cm and CD = 5 cm
In ΔADB and ΔCDB,
∠ADB = ∠CDB ...[Each equal to 90°]
And ∠BAD = ∠DBC ...[Each equal to 90 – ∠C]
∴ ΔDBA ∼ ΔDCB ...[By AAA similarity criterion]
Then, `("DB")/("DA") = ("DC")/("DB")`
⇒ DB2 = DA × DC
⇒ DB2 = 4 × 5
⇒ DB = `2sqrt(5)` cm
In right angled ΔBDC,
BC2 = BD2 + CD2 ...[By pythagoras theorem]
⇒ BC2 = `(2sqrt(5))^2 + (5)^2`
= 20 + 25
= 45
⇒ BC = `sqrt(45) = 3sqrt(5)`
Again, ΔDBA ∼ ΔDCB,
∴ `("DB")/("DC") = ("BA")/("BC")`
⇒ `(2sqrt(5))/5 = ("BA")/(3sqrt(5))`
∴ BA = `(2sqrt(5) xx 3sqrt(5))/5` = 6 cm
Hence, BD = `2sqrt(5)` cm and AB = 6 cm.
APPEARS IN
RELATED QUESTIONS
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

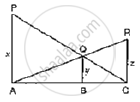
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
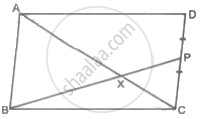
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).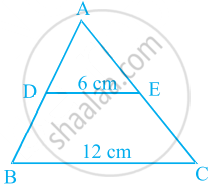
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC