Advertisements
Advertisements
प्रश्न
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.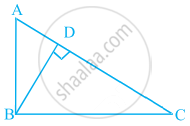
उत्तर
Given, ΔABC in which ∠B = 90° and BD ⊥ AC
Also, AD = 4 cm and CD = 5 cm
In ΔADB and ΔCDB,
∠ADB = ∠CDB ...[Each equal to 90°]
And ∠BAD = ∠DBC ...[Each equal to 90 – ∠C]
∴ ΔDBA ∼ ΔDCB ...[By AAA similarity criterion]
Then, `("DB")/("DA") = ("DC")/("DB")`
⇒ DB2 = DA × DC
⇒ DB2 = 4 × 5
⇒ DB = `2sqrt(5)` cm
In right angled ΔBDC,
BC2 = BD2 + CD2 ...[By pythagoras theorem]
⇒ BC2 = `(2sqrt(5))^2 + (5)^2`
= 20 + 25
= 45
⇒ BC = `sqrt(45) = 3sqrt(5)`
Again, ΔDBA ∼ ΔDCB,
∴ `("DB")/("DC") = ("BA")/("BC")`
⇒ `(2sqrt(5))/5 = ("BA")/(3sqrt(5))`
∴ BA = `(2sqrt(5) xx 3sqrt(5))/5` = 6 cm
Hence, BD = `2sqrt(5)` cm and AB = 6 cm.
APPEARS IN
संबंधित प्रश्न
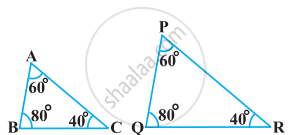
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
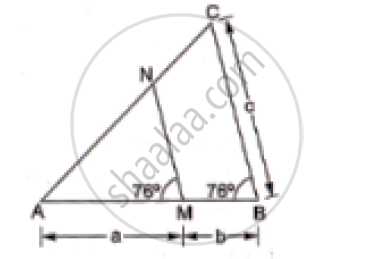
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.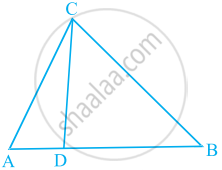
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

