Advertisements
Advertisements
प्रश्न
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
उत्तर
Let A be the position of the street bulb fixed on a pole AB = 6 m and CD = 1.5 m be the height of a woman and her shadow be ED = 3 m.
Let distance between pole and woman be x m.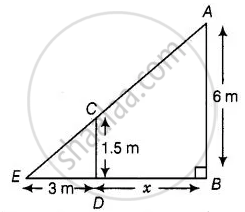
Here, woman and pole both are standing vertically.
So, CD || AB
In ΔCDE and ΔABE,
∠E = ∠E ...[Common angle]
∠ABE = ∠CDE ...[Each equal to 90°]
∴ ΔCDE ∼ ΔABE ...[By AAA similarity criterion]
Then, `("ED")/("EB") = ("CD")/("AB")`
⇒ `3/(3 + x) = 1.5/6`
⇒ 3 × 6 = 1.5(3 + x)
⇒ 18 = 1.5 × 3 + 1.5x
⇒ 1.5 = 18 – 4.5
∴ x = `(13.5)/1.5` = 9 m
Hence, she is at the distance of 9 m from the base of the pole.
APPEARS IN
संबंधित प्रश्न
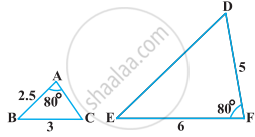
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
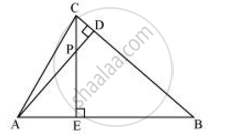
ΔAEP ∼ ΔCDP
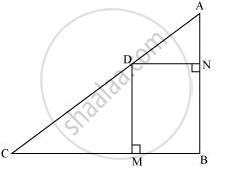
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

