Advertisements
Advertisements
प्रश्न
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

उत्तर
Given: Chord PQ || tangent AB
∴ ∠Q = ∠QDB = 50° ......[Alternate interior angles]
And ∠CDB = ∠PRD ......[Alternate interior angles]
ADB is a tangent at point D and CD is the circle's radius.
Thus, ∠CDB = 90° ......[Tangent theorem]
⇒ ∠CDQ + ∠QDB = 90°
⇒ ∠CDQ + 50° = 90°
⇒ ∠CDQ = 90° – 50° = 40°
CR is a perpendicular to the chord PQ, so it bisects PQ.
Thus, ∠PRC = 90° and PR = QR
Now, in ΔDRP and ΔDRQ
PR ≅ QR .....[Proved above]
∠DRP ≅ ∠DRQ ......[Each 90°]
DR ≅ DR ......[Common side]
Thus ΔDRP ≅ ΔDRQ .....[By SAS criterion of congruence)
So, ∠P ≅ ∠Q .....[C.A.C.T.]
⇒ ∠P = 50° .....[∵ ∠Q = 50°]
Now, the sum of the interior angles in a triangle is 180°.
Thus, ∠P + ∠PRD + ∠RDP = 180°
50° + 90° + ∠RDP = 180°
∠RDP = 180° – 50° – 90° = 40°
Now, ∠PDQ = ∠RDP + ∠RDQ
⇒ ∠PDQ = 40° + 40° = 80°
Hence, ∠PDQ = 80°.
APPEARS IN
संबंधित प्रश्न
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
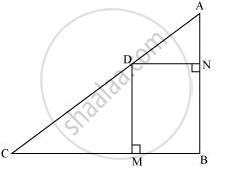
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
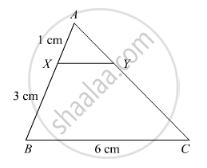
In the following figure, XY || BC. Find the length of XY.
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
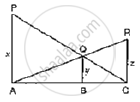
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
In the given figure, value of x(in cm) is

In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?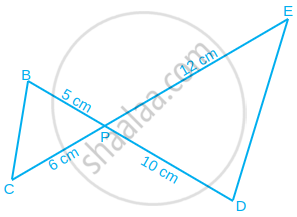
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
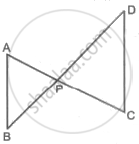
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.
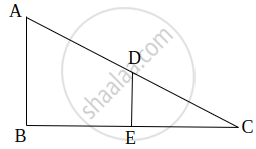
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
