Advertisements
Advertisements
प्रश्न
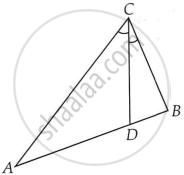
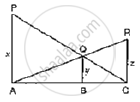
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
उत्तर
 |
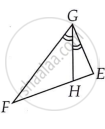 |
Given:
(i) ΔABC ∼ ΔFEG
∠A = ∠F ...(1)
∠B = ∠E ...(2)
∠C = ∠G ...(3)
The sides opposite to equal angles are essentially equal.
`"CD"/"GH" = "AC"/"FG"`
(ii) In ΔDCB and ΔHGE
In equation (2),
∠B = ∠E
In equation (3),
∠C = ∠G
∠BCD = ∠EGH
AA by similarity criterion
∆DCB ∼ ∆HGE
(iii) In ΔDCA and ΔHGF
In Equation (1)
∠A = ∠F
In equation (3),
∠C = ∠G
∠ACD = ∠FGH
AA by similarity criterion
∆DCA ∼ ∆HGF
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
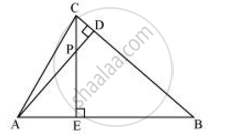
ΔAEP ∼ ΔCDP
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
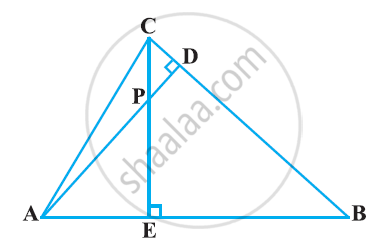
ΔAEP ∼ ΔADB
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
State the two properties which are necessary for given two triangles to be similar.
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.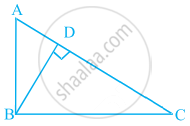
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?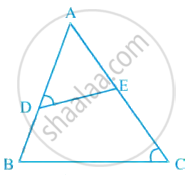
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
