Advertisements
Advertisements
प्रश्न
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

उत्तर
Given: AP ⊥ BC, BQ ⊥ AC
Now, in ΔAPC and ΔBQC
∠APC ≅ ∠BQC ......[Each equal to 90°]
∠ACP ≅ ∠BCQ .....[Common angle]
∴ By AA criterion of similarity,
ΔAPC ∼ ΔBQC
So, `(AP)/(AC) = (BQ)/(BC)` ......[C.S.S.T.]
Here, AP = 7, BQ = 8, BC = 12
Substituting the values,
`7/(AC) = 8/12`
⇒ AC × 8 = 7 × 12
⇒ AC = `(7 xx 12)/8` = 10.5
Hence, the value of AC is 10.5.
APPEARS IN
संबंधित प्रश्न
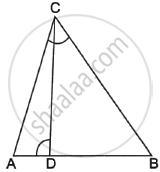
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
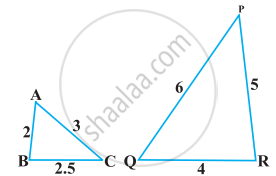
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
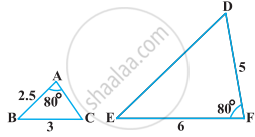
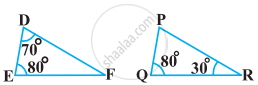
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
In the following figure, AB || QR. Find the length of PB.

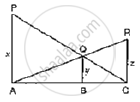
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
State the AAA-similarity criterion
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.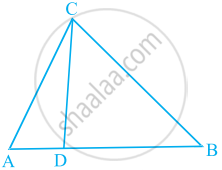
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
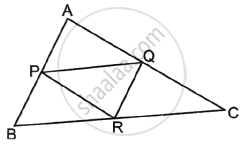
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.