Advertisements
Advertisements
प्रश्न
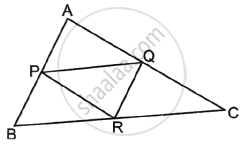
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
उत्तर
Given: ABC is a triangle and P, Q and R are the midpoints of sides AB, AC, and BC, respectively.
To prove: ΔABC is divided into 4 congruent triangles.
Proof: P and Q are the mid-points of AB and AC of ΔABC.
So, PQ || BC ......[Line segment joining the mid-points of two sides of a triangle is parallel to the third side]
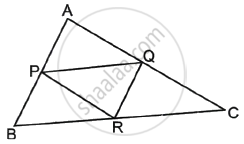
Similarly, PR || AC and QR || AB
In PQRB, PB || QR and PQ || BR ......[Parts of parallel lines are parallel]
i.e., Both opposite pairs of sides are parallel.
As a result, PQRB is a parallelogram.
As a result, PR is a diagonal of the parallelogram PQRB.
So, ΔPBR ≅ ΔPQR .....[A diagonal of a parallelogram divides it into two congruent triangles.] .....(i)
APRQ is also a parallelogram.
So, ΔAPQ ≅ ΔPQR .....(ii)
PQRC is also a parallelogram.
So, ΔPQR ≅ ΔQRC ......(iii)
From equations (i), (ii) and (iii),
ΔPBR ≅ ΔPQR ≅ ΔAPQ ≅ ΔQRC
As a result, all four triangles are congruent.
Hence Proved.
APPEARS IN
संबंधित प्रश्न
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
In the following figure, AB || QR. Find the length of PB.

In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
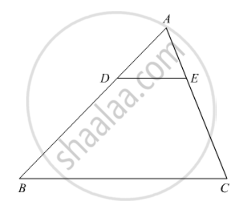
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
In the given figure MN|| BC and AM: MB= 1: 2
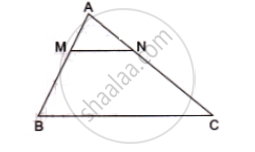
find ` (area(ΔAMN))/(area(ΔABC))`
In the given figure, value of x(in cm) is

In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

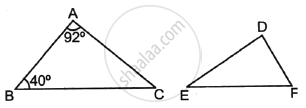
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
