SSC (English Medium)
SSC (Marathi Semi-English)
Academic Year: 2024-2025
Date: मार्च 2025
Advertisements
General Instructions :
- All questions are compulsory.
- Use of a calculator is not allowed.
- The numbers to the right of the questions indicate full marks.
- In case of MCQs (Q. No. 1(A)) only the first attempt will be evaluated and will be given credit.
- For every MCQ, the correct alternative (A), (B), (C) or (D) with subquestion number is to be written as an answer.
- Draw proper figures for answers wherever necessary.
- The marks of construction should be clear. Do not erase them.
- Diagram is essential for writing the proof of the theorem.
Find the coordinates of the mid-point of the line segment with points A(– 2, 4) and B(–6, –6) on both ends.
(4, –1)
(–4, –1)
(4, 1)
(– 4, 1)
Chapter: [0.05] Co-ordinate Geometry
In the figure, line l is parallel to X-axis. Which of the following statement is true?
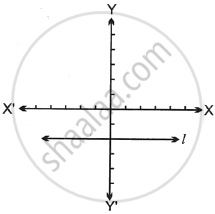
The slope is zero.
The slope cannot be determined.
The slope is positive.
The slope is negative.
Chapter: [0.05] Co-ordinate Geometry
If sec θ = `1/2`, what will be the value of cos θ?
2
1
3
5
Chapter: [0.06] Trigonometry
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
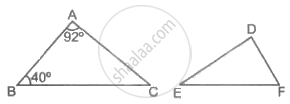
52°
92°
40°
48°
Chapter: [0.01] Similarity
The coordinates of two points are P(4, 5) and Q(–1, 6). Find the difference between their abscissas.
Chapter: [0.05] Co-ordinate Geometry
In ΔABC, ∠ABC = 90° and ∠ACB = θ. Then write the ratios of sin θ and tan θ from the figure.
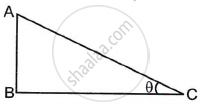
Chapter: [0.06] Trigonometry
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
Chapter: [0.03] Circle
If the coordinate of point A on the number line is –1 and that of point B is 6, then find d(A, B).
Chapter: [0.05] Co-ordinate Geometry
Advertisements
From the top of building AB, a point C is observed on the ground whose angle of depression is 60° and which is at a distance of 40 m from the base of the building. Complete the following activity to find the height of building AB.
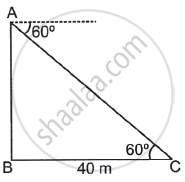
From figure, BC = `square`, ∠ACB = `square`
In ΔACB,
tan `square = square/(BC)`
⇒ `square = square/square`
⇒ `square = square`
Hence, the height of the building AB is `square`.
Chapter: [0.06] Trigonometry
Find the total surface area of frustum, if its radii are 15 cm and 7 cm. Also, the slant height of the frustum is 14 cm.
Radii of the frustum = `square` cm and `square` cm
Slant height of the frustum = `square` cm
Total surface area = `π[(r_1^2 + r_2^2 + (r_1 + r_2)l]`
= `22/7 [square + square + (square + square) square]`
= `22/7 (square)`
= `square` cm2
Hence, the total surface area of the frustum is `square`.
Chapter: [0.07] Mensuration
If the length of the diagonal of a cube is `5sqrt(3)` cm, find the total surface area.
Length of the diagonal of the cube = `square`
So, `square` = `5sqrt(3)`
⇒ Side = `square`
Total surface area of cube = `square`
= `square` × `square` × `square`
= `square` cm2
Hence, the total surface area is `square`.
Chapter: [0.07] Mensuration
In the following figure, XY = 10 cm and LT = 4 cm. Find the length of XT.
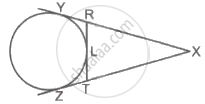
Chapter: [0.03] Circle
Point C divides the line segment whose points are A(4, –6) and B(5, 9) in the ratio 2:1. Find the coordinates of C.
Chapter: [0.05] Co-ordinate Geometry
Find the slope of the line passing through given points G(3, 7) and K(–2, –3).
Chapter: [0.05] Co-ordinate Geometry
There is a ladder of length 32 m which rests on a pole. If the height of pole is 18 m, determine the distance between the foot of ladder and the pole.
Chapter: [0.02] Pythagoras Theorem
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

Chapter: [0.01] Similarity
Advertisements
Determine whether the following points are collinear. A(–1, –1), B(0, 1), C(1, 3)
Given: Points A(–1, –1), B(0, 1) and C(1, 3)
Slope of line AB = `(square - square)/(square - square) = square/square` = 2
Slope of line BC = `(square - square)/(square - square) = square/square` = 2
Slope of line AB = Slope of line BC and B is the common point.
∴ Points A, B and C are collinear.
Chapter: [0.05] Co-ordinate Geometry
Prove that: cot θ + tan θ = cosec θ·sec θ
Proof: L.H.S. = cot θ + tan θ
= `square/square + square/square` ......`[∵ cot θ = square/square, tan θ = square/square]`
= `(square + square)/(square xx square)` .....`[∵ square + square = 1]`
= `1/(square xx square)`
= `1/square xx 1/square`
= cosec θ·sec θ ......`[∵ "cosec" θ = 1/square, sec θ = 1/square]`
= R.H.S.
∴ L.H.S. = R.H.S.
∴ cot θ + tan θ = cosec·sec θ
Chapter: [0.06] Trigonometry
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
Chapter: [0.06] Trigonometry
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
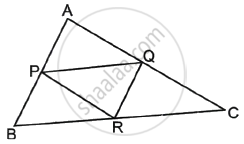
Chapter: [0.01] Similarity
Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
Chapter: [0.04] Geometric Constructions [0.05] Co-ordinate Geometry
In the given figure, a rectangle ABCD is inscribed inside a semi-circle of radius 10 cm. Using the dimensions given in the figure, determine the area of the shaded region.
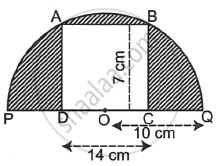
Chapter: [0.07] Mensuration
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

Chapter: [0.01] Similarity
In an equilateral triangle PQR, prove that PS2 = 3(QS)2.
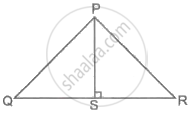
Chapter: [0.02] Pythagoras Theorem
The radius of a metallic sphere is 8 cm. It was melted to make a wire of diameter 6 mm. Find the length of the wire.
Chapter: [0.07] Mensuration
In the given figure, triangle PQR is right-angled at Q. S is the mid-point of side QR. Prove that QR2 = 4(PS2 – PQ2).

Chapter: [0.02] Pythagoras Theorem
The perimeter of an arc of radius 4.2 cm is 12.8 cm. Determine the angle subtended by the arc at the centre of circle.
Chapter: [0.07] Mensuration
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 10th Standard Board Exam Geometry Mathematics 2 with solutions 2024 - 2025
Previous year Question paper for Maharashtra State Board 10th Standard Board Exam Geometry Maths 2-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Geometry Mathematics 2, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 10th Standard Board Exam.
How Maharashtra State Board 10th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Geometry Mathematics 2 will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
