Advertisements
Advertisements
प्रश्न
From the top of building AB, a point C is observed on the ground whose angle of depression is 60° and which is at a distance of 40 m from the base of the building. Complete the following activity to find the height of building AB.
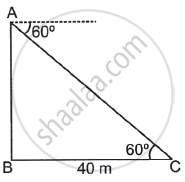
From figure, BC = `square`, ∠ACB = `square`
In ΔACB,
tan `square = square/(BC)`
⇒ `square = square/square`
⇒ `square = square`
Hence, the height of the building AB is `square`.
उत्तर
From figure, BC = 40 m, ∠ACB = 60°
In ΔACB,
tan 60° = `bb(AB)/(BC)`
⇒ `bbsqrt(3) = bb(AB)/bb40`
⇒ `bb(AB) = bb(40sqrt(3))`
Hence, the height of the building AB is `bb(40sqrt(3) m)`.
APPEARS IN
संबंधित प्रश्न
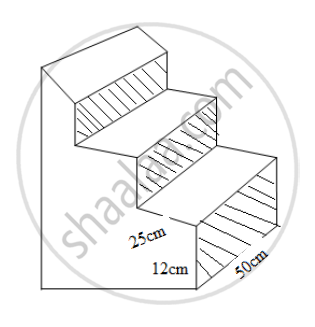
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
Read the following passage:
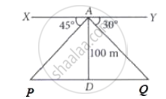
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ