Advertisements
Advertisements
प्रश्न
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
उत्तर
Consider the following figure:
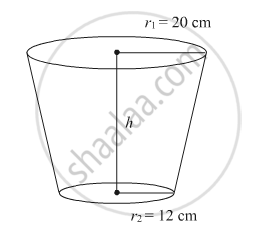
Given:
Volume of the frustum is 12308.8 cm3.
Radii of the top and bottom are r1 = 20 cm and r2 = 12 cm, respectively.
Volume of the frustum is given by
V=`1/3`πh(r12+r22+r1r2)
12308.8×3=πh(202+122+20×12)
12308.8×3=πh(400+144+240)
12308.8×3=πh(784)
`(12308xx3)/(3.14xx784)=h`
`(3920xx3)/784=h`
15cm = h
Hence, height of the frustum is 15 cm.
Now,
Metal sheet required to make the frustum = Curved surface area + Area of the base of the frustum
Curved surface area of the frustum =π(r1+r2)l, where l = `sqrt(h^2+(r_1-r_2)^2)`
`l = sqrt(15^2+(20-12)^2)`
`=sqrt(225+64)`
=`sqrt289`
=17 cm
Curved surface area of the frustum.
=π(20+12)17
=544×3.14
=1708.16 cm2
Area of the base =π122=144×3.14=452.16 cm2
∴ Metal sheet required to make the frustum=1708.16+452.16=2160.32 cm2
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
