Advertisements
Advertisements
Question
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
Solution
Consider the following figure:
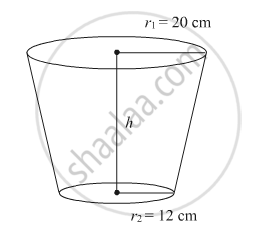
Given:
Volume of the frustum is 12308.8 cm3.
Radii of the top and bottom are r1 = 20 cm and r2 = 12 cm, respectively.
Volume of the frustum is given by
V=`1/3`πh(r12+r22+r1r2)
12308.8×3=πh(202+122+20×12)
12308.8×3=πh(400+144+240)
12308.8×3=πh(784)
`(12308xx3)/(3.14xx784)=h`
`(3920xx3)/784=h`
15cm = h
Hence, height of the frustum is 15 cm.
Now,
Metal sheet required to make the frustum = Curved surface area + Area of the base of the frustum
Curved surface area of the frustum =π(r1+r2)l, where l = `sqrt(h^2+(r_1-r_2)^2)`
`l = sqrt(15^2+(20-12)^2)`
`=sqrt(225+64)`
=`sqrt289`
=17 cm
Curved surface area of the frustum.
=π(20+12)17
=544×3.14
=1708.16 cm2
Area of the base =π122=144×3.14=452.16 cm2
∴ Metal sheet required to make the frustum=1708.16+452.16=2160.32 cm2
APPEARS IN
RELATED QUESTIONS
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
