Advertisements
Advertisements
Question
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
Solution
According to given information, we have the following figure
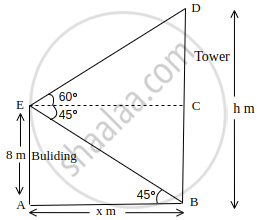
Let BD = h m and AB = x m
Then, CD = h – 8 ...(∵ BC = 8 m)
Also, In ΔEAB, we have
tan45° = `8/x`
⇒ 1 = `8/x`
⇒ x = 8 m
Similarly, In ΔDCE, we have
tan60° = `(CD)/(EC)`
⇒ `sqrt(3) = (h - 8)/x` ...(∵ EC = AB = x m)
⇒ `sqrt(3)x` = h – 8
⇒ `8sqrt(3)` = h – 8 ...(∵ x = 8 m)
⇒ h = `8(sqrt(3) + 1)`
= 8 × 2.732
= 21.856 m
APPEARS IN
RELATED QUESTIONS
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

If a tower 30 m high, casts a shadow `10sqrt3` m long on the ground, then what is the angle of elevation of the sun?
A flag-staff stands on the top of a 5 m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flag-staff.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
The angle of elevation of the top of a tower from a point 20 meters away from its base is 45°. The height of the tower is ____________.
