Advertisements
Advertisements
Question
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
Options
ab
\[\sqrt{ab}\]
\[\frac{a}{b}\]
\[\sqrt{\frac{a}{b}}\]
Solution
Let h be the height of tower AB.
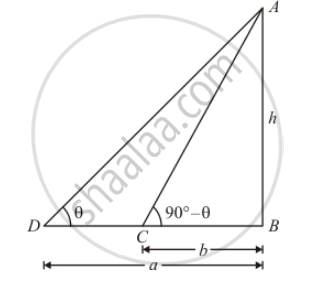
Given that: angle of elevation of top of the tower are `∠D=θ`and .`∠C=90°-θ`
Distance`BC=b` and `BD=a`
Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle, ABC
`tan D=(AB)/(BC)`
`⇒ tan (90°-θ)=h/b`
`⇒ cotθ=h/b`
Again in a triangle ABD,
`tan D=(AB)/(BD)`
`⇒ tan θ=h/a`
`⇒1/cot θ=h/a`
⇒ `b/h=h/a`
`⇒h^2=ab`
`⇒ h=sqrt(ab)`
Put `cotθ=h/b `
APPEARS IN
RELATED QUESTIONS
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
