Advertisements
Advertisements
Question
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
Solution
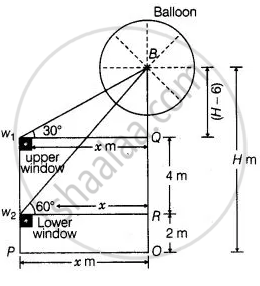
Let the height of the balloon from above the ground is H.
A and OP = w2R = w1Q = x
Given that, height of lower window from above the ground = w2P = 2 m = OR
Height of upper window from above the lower window = w1w2 = 4 m = QR
∴ BQ = OB – (QR + RO)
= H – (4 + 2)
= H – 6
And ∠Bw1Q = 30°
⇒ ∠Bw2R = 60°
Now, in ΔBw2R,
tan 60° = `"BR"/("w"_2"R") = ("BQ" + "QR")/x`
⇒ `sqrt(3) = (("H" - 6) + 4)/x`
⇒ `x = ("H" - 2)/sqrt(3)` ...(i)
And in ΔBw1Q,
tan 30° = `"BQ"/("w"_1"Q")`
tan 30° = `("H" - 6)/x = 1/sqrt(3)`
⇒ `x = sqrt(3)("H" - 6)` ...(ii)
From equations (i) and (ii),
`sqrt(3)("H" - 6) = (("H" - 2))/sqrt(3)`
⇒ 3(H – 6) = H – 2
⇒ 3H – 18 = H – 2
⇒ 2H = 16
⇒ H = 8
So, the required height is 8 m.
Hence, the required height of the balloon from above the ground is 8 m.
APPEARS IN
RELATED QUESTIONS
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
