Advertisements
Advertisements
प्रश्न
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
उत्तर
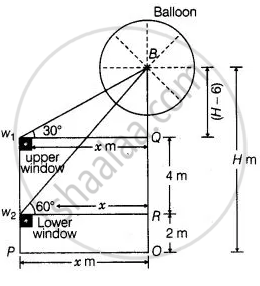
Let the height of the balloon from above the ground is H.
A and OP = w2R = w1Q = x
Given that, height of lower window from above the ground = w2P = 2 m = OR
Height of upper window from above the lower window = w1w2 = 4 m = QR
∴ BQ = OB – (QR + RO)
= H – (4 + 2)
= H – 6
And ∠Bw1Q = 30°
⇒ ∠Bw2R = 60°
Now, in ΔBw2R,
tan 60° = `"BR"/("w"_2"R") = ("BQ" + "QR")/x`
⇒ `sqrt(3) = (("H" - 6) + 4)/x`
⇒ `x = ("H" - 2)/sqrt(3)` ...(i)
And in ΔBw1Q,
tan 30° = `"BQ"/("w"_1"Q")`
tan 30° = `("H" - 6)/x = 1/sqrt(3)`
⇒ `x = sqrt(3)("H" - 6)` ...(ii)
From equations (i) and (ii),
`sqrt(3)("H" - 6) = (("H" - 2))/sqrt(3)`
⇒ 3(H – 6) = H – 2
⇒ 3H – 18 = H – 2
⇒ 2H = 16
⇒ H = 8
So, the required height is 8 m.
Hence, the required height of the balloon from above the ground is 8 m.
संबंधित प्रश्न
A tree is broken by the wind. The top of that tree struck the ground at an angle of 30° and at a distance of 30. Find the height of the whole tree
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
