Advertisements
Advertisements
प्रश्न
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
उत्तर
Given, height of building = 7 m
Let AC = h m and BD = x m
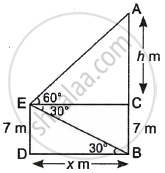
In ΔBDE,
tan 30° = `(ED)/(BD)`
`\implies = 1/sqrt(3) = 7/x`
`\implies` x = `7sqrt(3)` m
In ΔACE,
tan 60° = `(AC)/(CE)`
`\implies sqrt(3) = h/x` ...[∵ CE = BD]
`\implies` h = `xsqrt(3)`
= `7sqrt(3) xx sqrt(3)`
= 7 × 3
= 21 m
∴ Height of the tower = AB = AC + CB
= 21 + 7
= 28 m.
APPEARS IN
संबंधित प्रश्न
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
