Advertisements
Advertisements
प्रश्न
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
उत्तर
Given, height of tower = AB = 75 m
Let distance between the cars = CD = x m
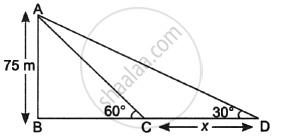
In ΔABC,
tan 60° = `(AB)/(BC)`
`\implies sqrt(3) = 75/(BC)` ...(∵ tan 60° = `sqrt(3)`)
`\implies` BC = `75/sqrt(3)`
= `(75sqrt(3))/3`
= `25sqrt(3)` m
In ΔABD,
tan 30° = `(AB)/(BD)`
`\implies 1/sqrt(3) = 75/(BC + CD)` ...`(∵ tan 30^circ = 1/sqrt(3))`
`\implies 1/sqrt(3) = 75/(25sqrt(3) + CD)`
`\implies 25sqrt(3) + CD = 75sqrt(3)`
`\implies` CD = `75sqrt(3) - 25sqrt(3)`
= `50sqrt(3)`
= 50 × 1.73
= 86.5 m
APPEARS IN
संबंधित प्रश्न
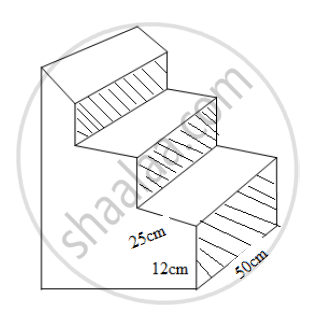
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
