Advertisements
Advertisements
प्रश्न
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
उत्तर
Given, height of tower = AB = 75 m
Let distance between the cars = CD = x m
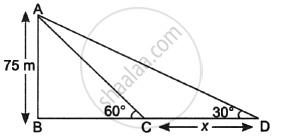
In ΔABC,
tan 60° = `(AB)/(BC)`
`\implies sqrt(3) = 75/(BC)` ...(∵ tan 60° = `sqrt(3)`)
`\implies` BC = `75/sqrt(3)`
= `(75sqrt(3))/3`
= `25sqrt(3)` m
In ΔABD,
tan 30° = `(AB)/(BD)`
`\implies 1/sqrt(3) = 75/(BC + CD)` ...`(∵ tan 30^circ = 1/sqrt(3))`
`\implies 1/sqrt(3) = 75/(25sqrt(3) + CD)`
`\implies 25sqrt(3) + CD = 75sqrt(3)`
`\implies` CD = `75sqrt(3) - 25sqrt(3)`
= `50sqrt(3)`
= 50 × 1.73
= 86.5 m
APPEARS IN
संबंधित प्रश्न
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
